適合度検定はvcdパッケージのgoodfit()関数で行う。
> t <- 0:5
> x <- c(8, 6, 8, 3, 4, 1)
> x <- matrix(c(x, t), nr = 6)
> library(vcd)
> result <- goodfit(x, type = "poisson", method = "MinChisq")
> result
Observed and fitted values for poisson distribution
with parameters estimated by `MinChisq'
count observed fitted pearson residual
0 8 5.1375937 1.262848928
1 6 9.0658624 -1.018235178
2 8 7.9988673 0.000400486
3 3 4.7049673 -0.786027501
4 4 2.0756111 1.335733618
5 1 0.7325299 -0.016953894
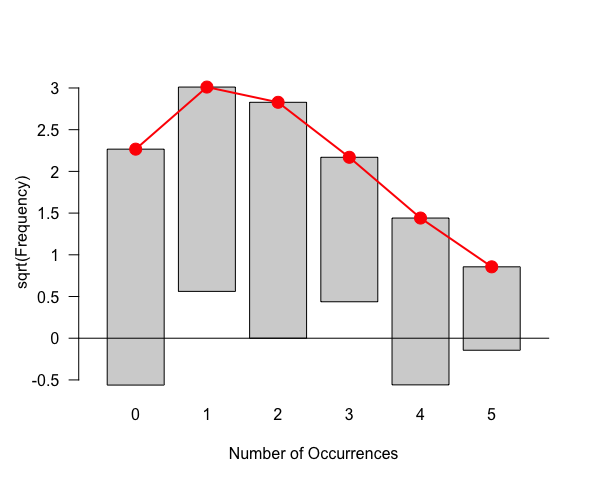
結果をplot()に渡すことで、結果を視覚的に判断することもできる。
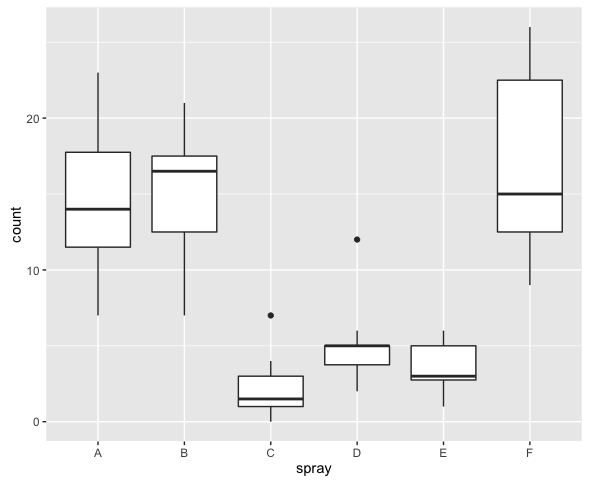
データセットInsectSpraysは殺虫剤ごとの死虫数*1をまとめたものである。このデータは平均値が大きいほど分散が大きく、ポアソン分布の特徴を持っているように見える。
ggplot(InsectSprays, aes(x = spray, y = count)) + geom_boxplot()
glm()による解析を行ってみる。
> result <- glm(count ~ spray, data = InsectSprays, family = "poisson")
> summary(result)
Call:
glm(formula = count ~ spray, family = "poisson", data = InsectSprays)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3852 -0.8876 -0.1482 0.6063 2.6922
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.67415 0.07581 35.274 < 2e-16 ***
sprayB 0.05588 0.10574 0.528 0.597
sprayC -1.94018 0.21389 -9.071 < 2e-16 ***
sprayD -1.08152 0.15065 -7.179 7.03e-13 ***
sprayE -1.42139 0.17192 -8.268 < 2e-16 ***
sprayF 0.13926 0.10367 1.343 0.179
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 409.041 on 71 degrees of freedom
Residual deviance: 98.329 on 66 degrees of freedom
AIC: 376.59
Number of Fisher Scoring iterations: 5
この結果から推定値を得るためには、例えばIntercept(=sprayA)であれば 、sprayBであれば
、sprayBであれば というようにやるのだが、まとめて求めるにはpredict()関数を使用する。
というようにやるのだが、まとめて求めるにはpredict()関数を使用する。
> pred <- predict(result, newdata = data.frame(spray = LETTERS[1:6]),
+ type = "response")
> pred
1 2 3 4 5 6
14.500000 15.333333 2.083333 4.916667 3.500000 16.666667
newdataには説明変数と同じ名前を持つ列に、予測したい説明変数の値をセットしたデータフレームを指定する。省略すると元のデータフレームの説明変数の値全てに対応する予測値が表示される。typeに"response"を指定することで、実際の予測値(上でexp()を使って計算した後の値)が表示される。指定しない場合は線形予測子の値(上でexp()に与えた中身)になる。
ついでに95%予測区間を求めてプロットしてみる。
> upr <- qpois(0.975, pred)
> lwr <- qpois(0.025, pred)
> ggplot(InsectSprays, aes(x = spray, y = count)) + geom_point() +
+ geom_pointrange(data = data.frame(spray = LETTERS[1:6], count = pred),
+ aes(ymin = lwr, ymax = upr), color = "blue")
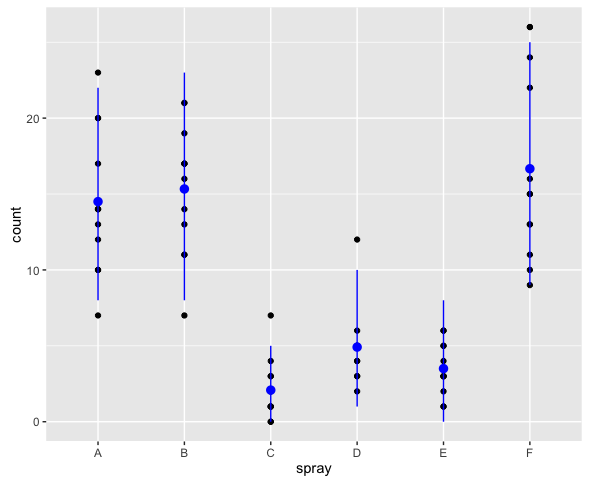
ちなみにこの予測区間はパラメータの標準誤差を考慮していないので、実際の予測区間よりたぶんちょっと狭い。そもそもこのような方法で予測区間を構成して良いものかどうかよく分からない。
オフセットによる調整法
まず、都道府県別の交通事故発生件数の一部を対象にポアソン回帰分析を行ってみる。
> accident <- c(45703, 8906, 7938, 12091, 7327, 9820, 11526, 6525)
> pref <- c("A福岡", "B佐賀", "C長崎", "D熊本",
+ "E大分", "F宮崎", "G鹿児島", "H沖縄")
> result1 <- glm(accident ~ pref, family = "poisson")
> result1
Call: glm(formula = accident ~ pref, family = "poisson")
Coefficients:
(Intercept) prefB佐賀 prefC長崎 prefD熊本 prefE大分
10.730 -1.635 -1.751 -1.330 -1.831
prefF宮崎 prefG鹿児島 prefH沖縄
-1.538 -1.378 -1.947
Degrees of Freedom: 7 Total (i.e. Null); 0 Residual
Null Deviance: 60920
Residual Deviance: 5.994e-12 AIC: 105.1
この結果を図示して解釈するためにまたpredict()を使ってみるが、typeに"terms"を指定すると、係数をスケールとした値が得られる。
具体的には"constant"属性に1つの値を持つベクトルが返ってくるが、constantの値とベクトルの各値を足したものが線形予測子である(result1のCoefficientsの値と比較してみると良い)。
> pred <- predict(result1, type = "terms")
> pred
pref
1 1.42600826
2 -0.20943048
3 -0.32449433
4 0.09630569
5 -0.40458953
6 -0.11173456
7 0.04844967
8 -0.52051473
attr(,"constant")
[1] 9.303911
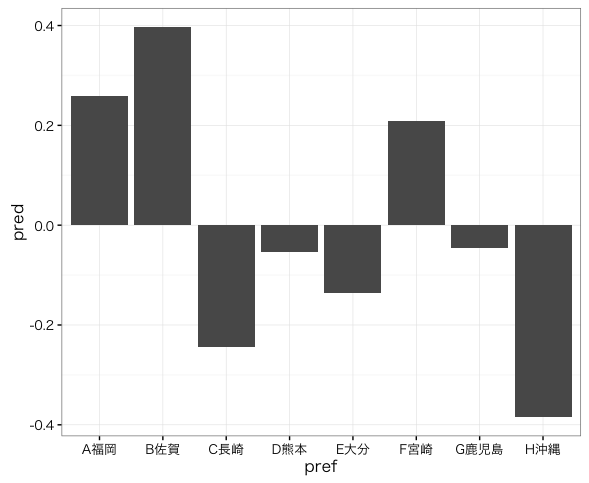
これをプロットしてみる。
ggplot(data.frame(pref, pred),
aes(x = pref, y = pred)) +
geom_bar(stat = "identity") +
theme_bw(base_family = "HiraKakuProN-W3")

圧倒的に福岡の係数が大きいが、これをもって福岡は交通事故が多いと判断して良いだろうか?
ここで、人口当たりの交通事故発生件数で解析することを試みる。
交通事故発生件数の平均を 、人口を
、人口を とすると、次のようなモデルを解析することになる。
とすると、次のようなモデルを解析することになる。

真数の商は対数の差であるので、右辺に を含めて解析することで
を含めて解析することで を解析することができる。
を解析することができる。 の様な項をオフセットと呼び、glmではoffset=に指定する。
の様な項をオフセットと呼び、glmではoffset=に指定する。
> pop <- c(5056, 859, 1453, 1828, 1203, 1143, 1730, 1373)
> result2 <- glm(accident ~ pref, offset = log(pop), family = poisson)
> result2
Call: glm(formula = accident ~ pref, family = poisson, offset = log(pop))
Coefficients:
(Intercept) prefB佐賀 prefC長崎 prefD熊本 prefE大分
2.20159 0.13712 -0.50356 -0.31235 -0.39484
prefF宮崎 prefG鹿児島 prefH沖縄
-0.05082 -0.30510 -0.64295
Degrees of Freedom: 7 Total (i.e. Null); 0 Residual
Null Deviance: 5699
Residual Deviance: 8.338e-12 AIC: 105.1
先ほどと同様にプロットしてみると、結果は違ったものとなる。
> pred <- predict(result2, type = "terms")
> ggplot(data.frame(pref, pred),
+ aes(x = pref, y = pred)) +
+ geom_bar(stat = "identity") +
+ theme_bw(base_family = "HiraKakuProN-W3")
この例ではもともとがフルモデルによる解析なのでoffsetを指定してもモデルが変化せず、従ってAICも変化しない*2。
過分散である場合の解析方法
ポアソン分布におけるパラメータ が、観測のたびにガンマ分布に従って変動すると仮定する。
が、観測のたびにガンマ分布に従って変動すると仮定する。
このような仮定にもとづいて乱数を発生させると、平均よりも分散が大きくなる。
> lambda <- rgamma(n, shape = 5, scale = 3)
> y <- rpois(n, lambda)
> mean(y)
[1] 13.15
> var(y)
[1] 49.08158
このような状況を過分散と呼ぶ。
次に、過分散する用量反応データを人工的に作成する。
n = 20
v = 3
dose <- 0:4 * 5
x <- rep(dose, n)
a <- exp(3 + 0.05 * dose) / v
lambda <- rgamma(5 * n, shape = a, scale = v)
y <- rpois(5 * n, lambda)
dataNB <- data.frame(x, y)
xで層別してプロットするとともに平均・分散を求めてみる。
> ggplot(dataNB, aes(x = x, y = y)) + geom_boxplot(aes(group = x))
> library(dplyr)
> dataNB %>% group_by(x) %>% summarize(mean(y), var(y))
x mean(y) var(y)
<dbl> <dbl> <dbl>
1 0 18.60 43.09474
2 5 23.80 97.74737
3 10 30.70 56.22105
4 15 49.45 134.47105
5 20 52.70 212.64211
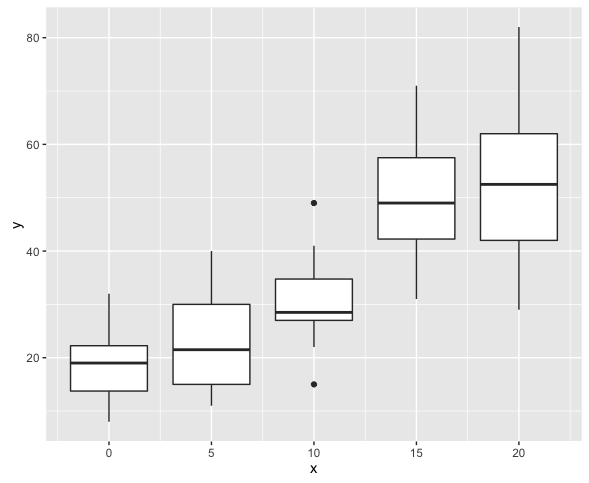
そのように作成したので当然ではあるが、過分散が確認できる。
このようなデータの解析には負の二項分布モデルを使用することができ、RではMASSパッケージのglm.nb()関数を用いる。使用方法はglm()とほとんど同じである。
>
> result <- glm.nb(y ~ x, data = dataNB)
>
> result2 <- glm(y ~ x, data = dataNB, family = poisson)
> result
Call: glm.nb(formula = y ~ x, data = dataNB, init.theta = 15.79541194,
link = log)
Coefficients:
(Intercept) x
2.91633 0.05636
Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
Null Deviance: 266.5
Residual Deviance: 102.7 AIC: 747.9
> result2
Call: glm(formula = y ~ x, family = poisson, data = dataNB)
Coefficients:
(Intercept) x
2.9285 0.0553
Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
Null Deviance: 825.1
Residual Deviance: 314.4 AIC: 845.6
ポアソン回帰分析に比べ、残差逸脱度、AIC共に小さくなっていることが分かる。
これもまたプロットしておこう。
ux <- seq(0, 20, by = 0.1)
pred <- predict(result, newdata = data.frame(x = ux),
type = "response")
upr <- qnbinom(0.975, size = result$theta, mu = pred)
lwr <- qnbinom(0.025, size = result$theta, mu = pred)
ggplot(data.frame(ux, pred),aes(x = ux, y = pred)) +
geom_line() +
geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.25) +
geom_point(data = dataNB, aes(x = x, y = y))
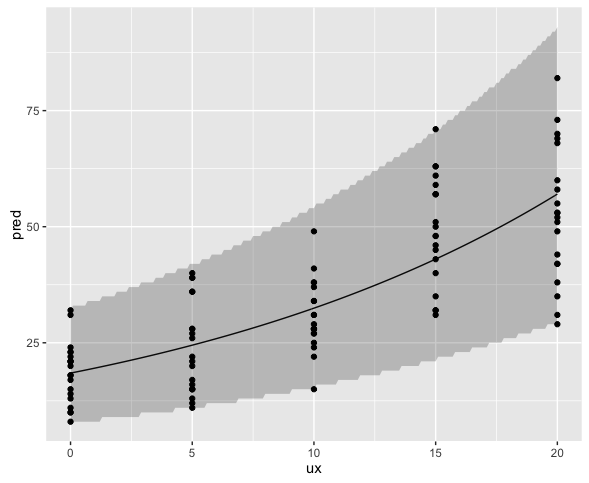
プロットの結果から見てもさほど問題は無いと思うが、予測区間はパラメータの標準誤差を考慮していないのできっと少し狭い。
























