なんでn-1なんですか - もうカツ丼はいいよな

不偏分散はなぜnではなくn-1で割るのか、という問題。

以前似たようなことやったけどきちんと証明していなかったのと今ならどう書くか試してみたかったので。

証明をする

確率変数 $X$ の実現値を $X_i$ 、平均を $\bar{X}$ とする。

まず、 $\sum\left(X_i - \bar{X}\right)^2$ の期待値を求めよう。

任意の数 $\mu$ を足して引く。

$E\left[\sum\left((X_i - \mu) - (\bar{X} - \mu)\right)^2\right]$

ここで、

$\sum(x_i - \bar{x})^2 = \sum x_i^2 - n\bar{x}^2$

であることに注意すれば、

$\sum E \left[ (X_i - \mu)^2 \right] - nE \left[ (\bar{X} - \mu)^2 \right]$

$\sum E \left[ (X_i - \mu)^2 \right] - nE \left[ \left( \frac{1}{n} \sum (X_i - \mu) \right)^2 \right]$

ここで任意の数 $\mu$ が母平均に等しかったとすれば、

$\sum E \left[ (X_i - \mu)^2 \right] = \sigma^2$

であるので、

$n\sigma^2 - \sigma^2 = (n-1)\sigma^2$

従って、 $\sigma^2$ の不偏推定量 $\hat{\sigma^2}$ は

$\hat{\sigma^2} = \frac{1}{n-1}\sum\left(X_i - \bar{X}\right)^2$

となる。

証明をしない

標準正規分布からのサンプリングに対し、nで割った場合とn-1で割った場合の分散の分布をシミュレーションしてプロットしてみよう。

library(dplyr)
library(ggplot2)

# (n-1)/nを乗ずることでnで割った場合の分散を求める
varp <- function(x){
  var(x) * (length(x) - 1)/length(x)
}

# n = 2:20において各1000回ずつvar(rnorm(n))及びvarp(rnorm(n))を求める
d <- data.frame()
N <- 1000
for(n in 2:20){
  d <- rbind(d,
             data.frame(n = n,
                        type = "var",
                        var = replicate(N, var(rnorm(n)))))
  d <- rbind(d,
             data.frame(n = n+0.3, # プロット時にちょっと右にずらすため調整
                        type = "varp",
                        var = replicate(N, varp(rnorm(n)))))
}

ggplot(d, aes(x = n, y = var, color = type)) + 
  geom_point(alpha = 0.1) +
  stat_summary(fun.y = mean, geom = "line") + # 平均をプロット
  theme_classic() +
  geom_hline(yintercept = 1, lty = 2, col = "gray", alpha = 0.3) # 真の分散=1を示す線

f:id:Rion778:20170706233312p:plain

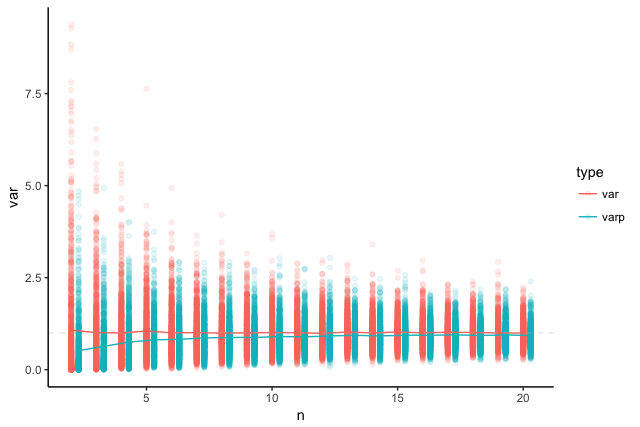
このようにnで割った分散の期待値は真の分散(=1)より少し小さくなる傾向がある。一方でn-1で割った場合の期待値は真の分散に一致する。また、nで割った場合でもnが大きくなれば真の分散に近づく傾向があることが分かる。実際、nで割った場合でもn→∞で真の分散に一致するので、nで割った分散は不偏推定量ではないが一致推定量ではある。