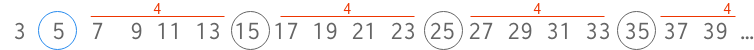少し前に某所でエラトステネスの篩の実装が正しくないとかなんとかで話題になったことがあった*1*2。そこでの結論が「アイデアとしては正しいが高速化のための実装としては間違い」みたいなところに落ち着いてしまってイマイチ腑に落ちなかったので少し調べた。
背景の整理
一般的に知られるエラトステネスの篩について
エラトステネスの篩は、次のようなアルゴリズムとして紹介されることが多い。
- 適当な上限を定める。
- 上限までの長さの論理値配列を作成し、全ての値を真で初期化する。
- 1番目の値を偽にする。
- 配列を先頭から順に見ていく。
- 値が真だったら、その値のインデックスの整数倍(1倍を除く)のインデックスにある値を偽にする。
- 例:3番目のインデックスであれば、6番目、9番目、12番目…の値を偽にする。
- このとき、確認する範囲をインデックスの二乗以降(3であれば9番目以降)にすると少し効率化できる。二乗より小さい値が合成数なら、今見ている値のインデックスより小さい約数が存在しているため。
- 4の操作を、最初にみつかるインデックスが1で定めた上限の平方根に達するまで行う。
- 最終的に論理値配列のなかで真になっている箇所に対応するインデックスの値が素数である。
要するに、素数の整数倍は合成数なので、素数リストから除外できるというのがポイント。
普通に(?)素数判定する場合とくらべて何が優れているかを比べるため、エラトステネスの篩を使わない簡単な素数判定について考えてみよう。
ある値nについて、素数かどうかを判定する素朴な方法は以下の全ての自然数で割ってみて、割り切れる値があるかどうか確認するというものである。この場合
回の計算が必要になる。
以下の素数が全て分かっているなら、
以下の自然数を
以下の素数に置き換えると少し効率化できる。この場合は
以下の素数個分の計算が必要になる。たとえば140であれば、自然数なら11個、素数なら5個の試し割りが必要になる。
一方、エラトステネスの篩は、各値について素因数の数と同じ回数だけ参照が発生する。例えばについて考えてみると、この値のインデックスは手順4において
- 2の倍数を偽にするとき
- 5の倍数を偽にするとき
- 7の倍数を偽にするとき
の3回だけ参照される。また、エラトステネスの篩で発生する操作はフラグの切り替えなので、試し割りより計算負荷が低い場合も多いだろう。
似非エラトステネスの篩
一方、似非エラトステネスの篩として指摘された解法は次のようなものだった。
- 適当な上限を定める。
- 2〜上限までの整数を列挙する。
- 列挙した整数のうち、最も小さいものを素数リストに加える。 もしこの値が上限の平方根を超えていたら終了。残っているものが素数。
- 列挙した整数すべてについて、3でリストに加えた素数で割り切れるかどうかを確認する。もし割り切れたら、整数のリストから除外する。
- 手順3に戻る。
雰囲気は似ているが、マズいのは手順4だ。残っている整数すべてについて注目している素数での試し割りをしているので、各値に対して発生する計算回数が素数の個数分になる。本来のエラトステネスの篩では素数に対する参照は発生しないので、ここで余分な参照と計算が発生してしまうわけである。
さらに良くないことに、上限の平方根より小さい値の場合、もしその値が素数ならその値より小さいすべての素数で試し割りされることになる。つまり、この方法は普通に素数を列挙しながら試し割りをするより計算回数が多いのである。「高速化に寄与しない」どころではない。
「アイデアとしては正しい」のかどうか
この方法が少なくとも効率性の面では誤っているというのは既に指摘されており、記事も修正されている。 だが、当初の指摘で「エラトステネスの篩のアイデアの実装としては正しい」と記述があったためか、修正文も「エラトステネスの篩のアイデアを用いているが高速化に寄与しない」というような説明になっている。
しかし、本来のエラトステネスの篩は試し割りという作業が発生しない。というより、試し割りをせずに素数を列挙できるというのがポイントのように思える。「アイデアとして正しい」は本当に正しいのかどうか…?
そもそもエラトステネスの篩とは何だったか
一般的に知られるエラトステネスの篩は、現代人が理解しやすいように、プログラムで実装しやすいように整理されてしまっているのではないだろうか。似非エラトステネスの篩がアイデアとして正しいのかどうか、を考えるためには、そもそもエラトステネスの篩とは何だったのかを調べねばなるまい。
エラトステネス is 誰
エラトステネスは紀元前3世紀ごろのギリシャの数学・天文学者で、プトレマイオス3世のもと、アレキサンドリアの図書館長を努めた人物である。「エラトステネスの篩」以外にも、地球の大きさを初めて測定した人物として知られている。数学と天文学以外にも詩、哲学、歴史、スポーツにも秀で、オリンピックで5回の成功を収めたのでペンタクルスと呼ばれていたとか、ライバルたちが優れてはいるが1番ではないとしてベータ(2番目)とあだ名していたとかいう逸話がある。
エラトステネスの篩の初出
エラトステネスの篩について触れられている、知られている中で最も古い文献はニコマコスの『算術入門』(Introduction to Arithmetic)である。2巻からなるこの本の第1巻13章にエラトステネスの篩が出てくる。つまり、エラトステネスがそもそもどう言っていたのかは今となっては分からない。とはいえ、ニコマコスは1〜2世紀ごろの数学者である。エラトステネスから数百年後とはいえ、確認してみる価値はあるだろう。
ニコマコスはエラトステネスの篩をどう紹介したか
『算術入門』は1926年に英訳されたものにアクセスできる。
100年近く前ということに加え、現代的な数学の表現を使った文章ではないので非常に読みづらいが、ある程度雰囲気は分かる。
ニコマコスが算術入門で取り上げていたのは、2つの奇数が互いに素であるか、共通の因数を持つかどうかといったような話題の中だった。そこでエラトステネスの篩は、奇数を素数と合成数に分ける方法として次のように紹介されている。
- 全ての奇数を3から初めて、可能な限り長く列挙する。
- 最初の値(つまり3)に注目すると、これを因数に含む値が2つおきに現れる。
- 次の値(つまり5)に注目すると、これを因数に含む値は4つおきに現れる。
- さらに繰り返すと、7を因数に含む値は6つおきに現れる。
ここから次のことが分かる。
- 因数を含む数の間隔の大きさは、2〜無限大までの偶数の列をなす。
- 間隔の大きさは、注目している値の位置の2倍である。(あるいは注目している値-1である)
ニコマコスは証明を特に書いてないが、要するに注目している各値に奇数を順次掛けていっているだけなので、上の結果はほぼ自明だろう。
注目している値を因数として含む値に順次印をつけていくことを考えよう。
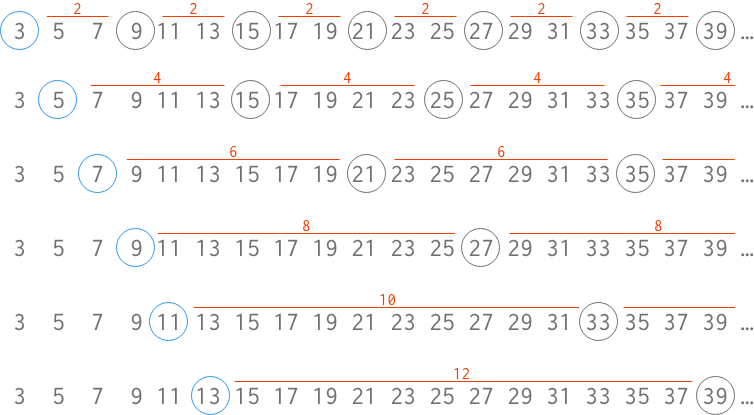
この表を見ていくと、「因数を含む」としてマークされていない(上図でいうと黒丸が付いていない)値がある。これらの値は自身と1以外に因数をもたないので、つまりこれが素数である(13章ではそもそも奇数に注目しているので、2は含まれていないことには注意)。13章の内容はこの後も続き、2つの奇数が互いに素であるかどうかを判定する方法が説明されるが、話題がそれるので省略する(※ユークリッドの互除法が紹介されている)。
結局どうなのか
ニコマコスの紹介によるエラトステネスの篩の要点は、注目している奇数を因数として含む値が、規則的な間隔で出現するという部分にある。つまり、「間隔を2つずつ増やしていく」という単純な操作によって、ある値が因数に含まれる値を列挙できるというのがポイントだ。
エラトステネスが実際にどう説明していたのかはわからなかったが、ニコマコスは「篩」の方法について因数が規則的に出現することを丁寧に例を挙げながら解説している。したがって、エラトステネスの篩はこの規則性を利用し、試し割りのような面倒な計算をすることなく素数を列挙できるという点にこそアイデアの要点があると言えるだろう。
試し割りを含む実装は、エラトステネスの篩のアイデアの実装としても正しいようには思えない、というのが結論である。
参考文献
- Nicomachus Intro to Arithmetic : Nicomachus : Free Download, Borrow, and Streaming : Internet Archive
- 本文中でも取り上げたニコマコスの「算術入門」の英訳。1926年の出版であるが、著者のMartin Luther D'Oogeはそれに先立つ1915年に急逝している。未完成であった彼の仕事をミシガン大学の同僚たちが完成させ出版に漕ぎ着けたらしい。
- 初等整数論9章
- エラトステネスの篩は少しだけ説明がある。エラトステネス自体の説明が少し詳しい。
- Sieve of Eratosthenes - Wikipedia
- エラトステネスの篩をニコマコスが紹介していることについて説明がある。
- https://tbasic.org/reference/old/ErSieve.html
- このサイト、環境によって文字化けして読みづらいかもしれないが、エラトステネスの篩について「ニコマコス(100頃)の「算術入門」第1巻13章にその記述がある」という一文が書いてある。この情報がなかったら調べる気にならなかった。