ロトカ・ヴォルテラの捕食式

捕食者と被食者の個体数は捕食を通じて互いに影響しており、時に双方の個体数が共振動することがある。例えば、カナダのカンジキウサギ(被食者)とカナダオオヤマネコ(捕食者)の個体数は、約10年の周期で共振動している。野外では気象条件などの影響を排除し切れないが、室内の実験系においても共振動は確認されているらしい。
個体数の共振動という現象は、理論的にはロトカ・ヴォルテラの捕食式を用いることで確認できる。
ロトカ・ヴォルテラの捕食式では以下の仮定をしている。
まず、捕食者、被食者がそれぞれ単独で存在していて、捕食-被食の関係が存在しない時、捕食される心配のない被食者は世代ごとにrの割合で個体数を増やし、獲物を得られない捕食者は世代ごといqの割合で死亡すると仮定する。被食者の個体数をN、捕食者の個体数をPとすると


と表現できる。
次に、単位時間あたりに捕食される被食者の数について、その数は捕食者が多いほど、または被食者が多いほど増加すると想定する。ここでは単純に捕食者と被食者の個体数の積に比例すると考える。捕食効率を表す比例定数をaとして、単位時間あたりaNPという数で被食者が捕食されるとする。また、捕食者は捕食することにより個体数を増加させられると想定し、1個体捕食するごとにfという割合で個体数を増すと仮定する。よって、捕食者の個体数は単位時間あたりfaNPずつ増える。これら捕食の影響を先程の式に組み込むと、上の式は次のようになる。


これをロトカ・ヴォルテラの捕食式と称する。
ここでそれぞれのパラメータを適当に設定してシミュレーションしてみると、個体数が振動する様子が観察できる。

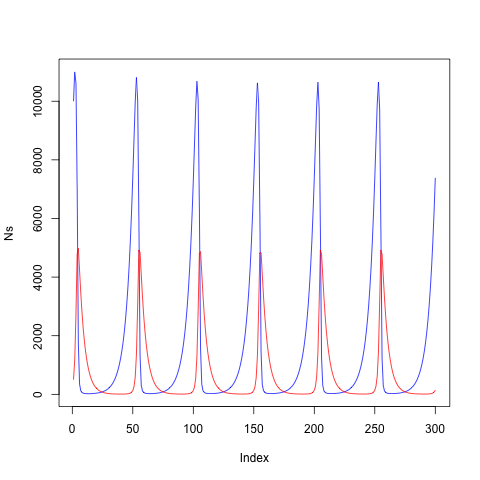
捕食者の個体数(Ps)と被食者の個体数(Ns)の関係をプロットすると、反時計回りに回る閉鎖円を見ることが出来る。

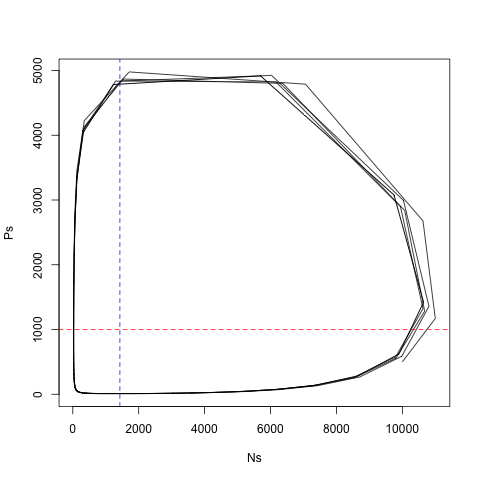
上の図で赤と青の点線で示した部分はそれぞれP=r/a、N=q/(fa)という値を示している。これらの値はロトカ・ヴォルテラの捕食式において、として求めたPの値、Nの値であり、それぞれNの値を増やしも減らしもしないPの値、Pの値を増やしも減らしもしないNの値という意味になる。P=r/aのときNが、N=q/(fa)とときPが最大となる。捕食者の数は被食者の数が最大になってから1/4周期遅れて最大となる。
なお、図はRで次のようにして描いた。

N <- 10000                              # 被食者の初期個体数
P <- 500                                # 捕食者の初期個体数
r <- 0.2                                # 被食者の増殖率
q <- 0.2                                # 捕食者死亡率
a <- 0.0002                             # 捕食効率
f <- 0.7                                # 捕食者の捕食数当たり産仔数

limit <- 300
Ns <- Ps <- numeric(limit)
for(i in 1:limit){
  Ns[i] <- N
  Ps[i] <- P
  N <- round(N + r*N - a*N*P)
  P <- round(P + f*a*N*P - q*P)
  if(is.nan(N) || is.nan(P) || N <= 0 || P <= 0) break
}

plot(Ns, type="l", col="blue")
lines(Ps, type="l", col="red")

plot(Ns, Ps, type="l")
abline(h = r/a, lty=2, col="red")
abline(v = q/(f*a), lty=2, col="blue")

また、捕食者と被食者の個体数をプロットして得られる閉鎖円の大きさは初期個体数に依存する。

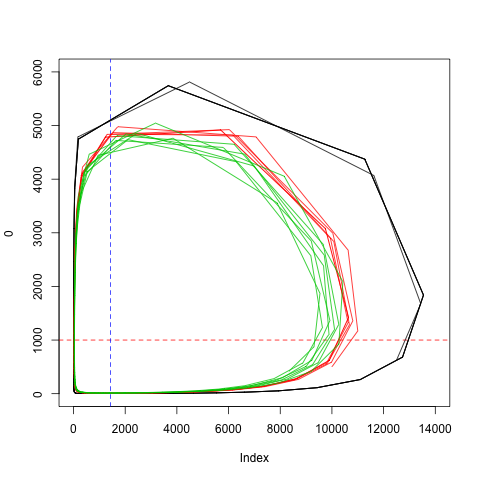
初期個体数は黒＞赤＞緑となっている。
この図は次のように描いた。

fun <- function(scale, col="black"){
  N <- 10000/scale                      # 被食者の初期個体数
  P <- 500/scale                        # 捕食者の初期個体数
  r <- 0.2                              # 被食者の増殖率
  q <- 0.2                              # 捕食者死亡率
  a <- 0.0002                           # 捕食効率
  f <- 0.7                              # 捕食者の捕食数当たり産仔数

  limit <- 300
  Ns <- Ps <- numeric(limit)
  for(i in 1:limit){
    Ns[i] <- N
    Ps[i] <- P
    N <- round(N + r*N - a*N*P)
    P <- round(P + f*a*N*P - q*P)
    if(is.nan(N) || is.nan(P) || N <= 0 || P <= 0) break
  }
  lines(Ns, Ps, type="l", col=col)
}
plot(0, ylim=c(0, 6000), xlim=c(0, 14000), type="n")
abline(h = r/a, lty=2, col="red")
abline(v = q/(f*a), lty=2, col="blue")
fun(0.8, 1)
fun(1.0, 2)
fun(1.2, 3)

ここでは単純な例として捕食者と被食者が1:1の関係にあるということを想定したが、捕食者が複数の獲物を餌とする多食性である場合や被食者が複数の種類の捕食者から狙われるような場合はより複雑な個体数変動となる。3種類以上の個体群を想定した場合、変動は非周期的な変動になってしまう。しかし非周期的とは言っても確率的に変動するわけではなく、密度に依存して個体数は変動する。

参考

• 生態学入門
• ロトカ・ヴォルテラの方程式 - Wikipedia