関連記事一覧
- メンデルの法則をめぐる論争について (1) - フィッシャーによる2つの指摘
- メンデルの法則をめぐる論争について (2) - 「1:1.7問題」は解決できる < イマココ
- メンデルの法則をめぐる論争について (3) - 「データができすぎている」は解決できない
- メンデルの法則をめぐる論争について (4) - 連鎖および近年のメンデルに対する評価
前回、メンデルの法則をめぐる論争の背景について説明し、フィッシャーの2つの指摘を紹介した。
今回はフィッシャーの指摘のうちの1つ、「F₂世代で優性型を示した個体の雑種型と不変型の分離比は2:1ではなく1.7:1として観測されるべきだがデータは2:1に近接している」という点について説明する。
メンデルの主張
フィッシャーの指摘内容を正確に理解するために、まずはメンデルの記述内容を再度確認する。
この問題の舞台となるのは、メンデルの論文中で「雑種の第二代目」と名付けられた節が扱う部分である。メンデルはこの節の頭に結論を書いているので、次に引用する。
第一代目に劣性の形質を有する型は、第二代目でも、その形質がもはや変わらず、その子孫まで不変である。
第一代目に優性の形質を有する型は、これと異なったふるまいをする。このうち、3分の2の部分は3:1の比で優性形質と劣性形質を示す子孫をつくり、雑種型とまったく同じふるまいを示す。3分の1の部分のみが優性形質で不変である。
(メンデル著, 岩槻邦男・須原準平訳『雑種植物の研究』)
ここで「第一代目」と言っているのは、雑種の子孫の第一代目という意味であり、現代風にいえばF₂世代のことを示す。F₂世代は優性形質と劣性形質が3:1の比率で分離する(分離の法則)。そのF₂世代についてそれぞれ自殖させてF₃世代を育成したとき、F₃世代の形質の現れ方のパターンでF₂世代が分類でき、その比率が一定の割合になるというのがメンデルの主張である。
- F₂世代で劣性形質を示したもの...子孫のすべてが劣性形質を示す
- F₂世代で優性形質を示したもの
- 2/3の個体は優性形質と劣性形質が3:1の比率で混ざった子孫を生ずる
- メンデルはこれを雑種、雑種型などと呼んでいるが、現代的にいえばヘテロ接合型である。
- 1/3の個体はすべての子孫が優性形質を示す
- メンデルはこれを不変の優性、不変型などと呼んだ。現代でいうホモ接合型である。
- 2/3の個体は優性形質と劣性形質が3:1の比率で混ざった子孫を生ずる
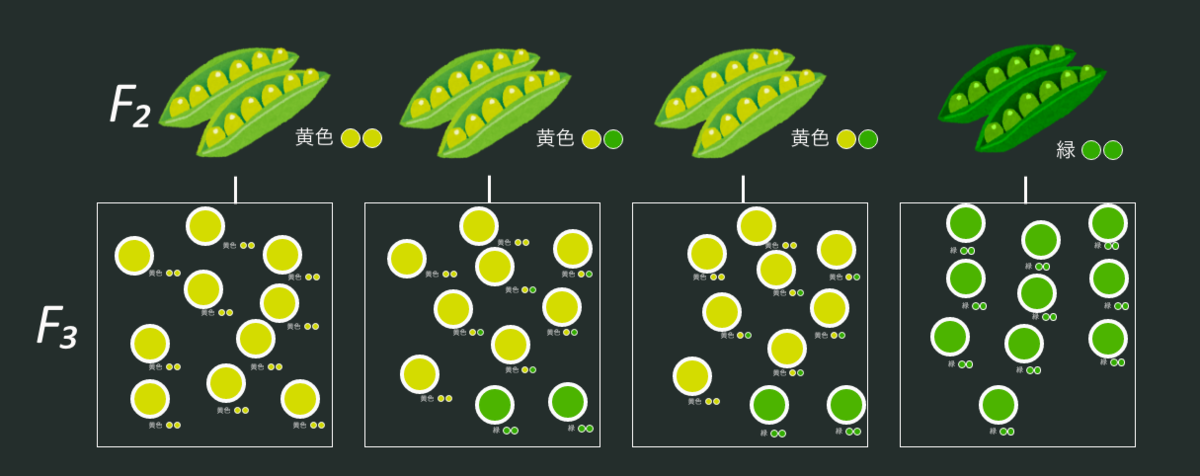
フィッシャーの指摘にも出てくる「2:1」という比率は、F₂世代で優性形質を示した個体の分類比率である。
フィッシャーの指摘
問題はメンデルの確認方法にある。ヘテロ接合型の子孫は優性形質と劣性形質を3:1の比率で示すのだから、子孫をn個体調査したとき、優性形質を示す個体の数は試行数n、確率θ = 0.75の二項分布に従うと考えられる。偶然にすべての個体が優性形質を示す確率は、[tex:0.75n]である。これはヘテロ接合型が偶然にホモ接合型と誤分類されてしまう確率である。すなわち、この確率のぶんだけ、ホモ接合型と判断される個体が理論値より過剰になるはずである。
メンデルが第一実験、第二実験と呼んでいる種子の形質(丸/しわ、黄/緑)を調べた実験では、(明示的には書かれていないものの)各個体から生じたすべての種子が調査されたと考えられる。1個体あたりの種子数は30程度と期待できるため、であり、誤分類率は2:1を狂わせるほどには大きくない。
問題は第三実験から第七実験である。この実験では種皮の色(=花の色)などの形質を扱っている。これらは植物個体を育成して調査する必要があるため、おそらく敷地面積や労力の都合から調査数が限定されている。調査方法についてのメンデルの記述を次に示す。
以下の実験のすべての場合に、第一代目に優性形質を示した100株の植物を選び、その優性の意味を調べるためにそれぞれの植物からの10粒の種子を播いて育てた。
(メンデル著, 岩槻邦男・須原準平訳『雑種植物の研究』)
メンデルは方法を示してはいるが、データについて細かくは提示していない。メンデルの記述を字義どおりに受け取れば、10粒を播種したのであるから、発芽不良などを考慮すると調査できた個体数は10個体より少ない可能性もある。しかし、いったんすべての種子が正常に発芽し、形質確認が可能になるまで生育したと仮定しよう。このとき、ヘテロ接合型の子孫が偶然にすべて優性形質を示してしまう確率は、すなわち約5.63%である。
つまり、優性形質を示したF₂世代の個体のうち、
- ホモ接合型と判断されるもの =
- ヘテロ接合型と判断されるもの =
である。であり、フィッシャーの指摘にある1:1.7というのはここにでてくる。すなわち、第三実験から第七実験の結果は、1:1.7に近くなければならない。実際のデータはどうなっているか確認してみよう。
| 実験 | ホモ接合型 | ヘテロ接合型 | 合計 | ヘテロ接合型/ホモ接合型 |
|---|---|---|---|---|
| 第三実験 | 36 | 64 | 100 | 1.777778 |
| 第四実験 | 29 | 71 | 100 | 2.448276 |
| 第五実験 | 40 | 60 | 100 | 1.500000 |
| 第六実験 | 33 | 67 | 100 | 2.030303 |
| 第七実験 | 28 | 72 | 100 | 2.571429 |
| 第五実験2回目 | 35 | 65 | 100 | 1.857143 |
| 合計 | 201 | 399 | 600 | 1.985075 |
第五実験に2回目があるのは、第五実験の結果が理論値からやや大きくずれたために実験が繰り返されたという事情による。
見て分かるように、合計結果は1:2にかなり近接している。しかも、6回の実験のうち5回でヘテロ接合型の比率が1.7より大きくなっており、1:2に対するバイアスがあるように見える。これはどうなのか、というのが指摘の要点となる。
なお、この部分だけでいえば期待比率1:2に対するχ²値は4.575、P=0.60程度であり、「データが良すぎる」というほどではない。期待比率1:1.7としてもχ²値は7.658、P = 0.264であり、逸脱が大きいわけでもない。この点に関してだけ注目すればフィッシャーの指摘はそもそもあまり筋が良くはないのである。ただし、実際にはフィッシャーの指摘はこれだけではないという点には注意しておくべきである。フィッシャーの指摘の要点は「データが全体として理論値に一致しすぎている」という点にあったが、ゆえにこの1:1.7からのバイアスを重要な証拠とみなしたのである。
指摘に対する反論1
フィッシャーの指摘を否定する仮説はいくつか提案されている。中でもSeidenfeld(1998)の説は「仮にメンデルが記述どおりの調査を行っていたとしても矛盾なく結果を説明できる」という点で優れているのでこれを紹介する。
Seidenfeldの説の要点は「メンデルはF₃の観察のみに基づいてF₂を分類したわけではない」というものである。
メンデルは「雑種の第二代目」に引き続いて「その後の雑種世代」と題した節を設けている。そこでは、第三世代(すなわちF₄)以降についての実験結果が示されている。形質によるが、4代〜6代まで実験を継続して行ったとの記述がある。ここでは、自殖を繰り返すにつれて相対的に雑種型の比率が少なくなる、というようなことが述べられているのみで、具体的なデータはほとんど示されていない。
しかし、ここで重要なのはメンデルがF₃世代以降も実験を続けたということである。この場合の自然な考え方は、「雑種の第二代目」の実験でF₂世代の分類に用いたF₃世代がそのまま育成して種子が採取され、F₄の親として使われたということである。
「その後の雑種世代」にはわずかに「三代目からはより少数の植物で実験を行った」との記述があるだけで、具体的な実験方法についての記述がなく詳しくは想像になるが、仮にF₃の各個体から1粒ずつの種子が採取されて育成されたとしよう。このとき、F₃の親はヘテロ接合型であったが、たまたまF₃の10株すべてが優性形質を示した例を考える。F₄まで考慮した場合の実際の誤分類率は次のように計算される。
- ヘテロ接合型に由来するF₃10個体が偶然にすべて優性形質を示す = 5.63%
- 10株のうち、平均的に2/3はヘテロ接合型であるから、F₃の種子1粒づつを栽培し、F₄がすべて偶然に優性形質を示す確率は、
- 1と2が同時に起こる確率は1%未満となる。
この場合でも誤分類は発生するのだが、上記のように比率1:2に対する影響は軽微となる。いまはF₃あたり1株と仮定したが、仮に2株であったら誤分類は1000株に1株程度の割合となる。そして、メンデルが実験に用いた庭の広さから考えても、このような実験は可能であったと判断されている。
指摘に対する反論2
他の反論として、「メンデルは10株以上を調査したのではないか」というものがある。仮にメンデルが10株ではなく15株を調査してのであれば、それだけで誤分類の確率は1%程度となる。この説も何度か言及されている。
この問題を考える上で重要なのは「それぞれの植物からの10粒の種子を播いて育てた」というメンデルの記述を字義どおりにとらえられるか、という点である。
フィッシャーは科学論文というものは記述について正確に解釈しなければならないという観点からこの説を否定した。しかし、実際にはメンデルの記述は正確とはいえず、正確さよりもわかりやすさを重視したと思われる部分がかなり多い。したがって、「10粒の種子を播いて育てた」とはいうものの、実際には発芽不良などを見越して10株よりもやや多い個体を調査していた可能性は十分に考えられる。
まとめ
- フィッシャーはデータの誤分類率から「1:1.7になるべき」という指摘をした。
- 実際にはメンデルの実験デザインまたは単なる記述の不正確から、「1:1.7」という比率が期待比率ではない可能性は十分に考えられる。
- したがって、この部分についてフィッシャーの指摘はさほど筋が良くなく、「メンデルのデータが曲げられている」と主張するには弱い。
今回はフィッシャーの指摘が部分的に正しくない可能性について説明した。しかし、繰り返しになるがフィッシャーの指摘はこれだけではない。そして、フィッシャーのもうひとつの指摘は、この「1:1.7問題」がなかったとしても(というよりないと仮定したうえで)成立するものである。したがって、この問題だけを否定しても「メンデルが捏造」の否定にはならないのである。次回はもうひとつの問題である「データが理論値に一致しすぎている」について説明する。
参考文献
- Seidenfeld, Teddy (1998) P's in a Pod: some recipes for cooking Mendel's data.