関連記事一覧
- メンデルの法則をめぐる論争について (1) - フィッシャーによる2つの指摘
- メンデルの法則をめぐる論争について (2) - 「1:1.7問題」は解決できる
- メンデルの法則をめぐる論争について (3) - 「データができすぎている」は解決できない < イマココ
- メンデルの法則をめぐる論争について (4) - 連鎖および近年のメンデルに対する評価
前々回、前回とメンデルの法則をめぐる法則を紹介し、前回はフィッシャーの2つの指摘のうち1つについて否定が可能という説明をした。今回はフィッシャーの指摘のもうひとつの要点である「データが理論値に一致しすぎている」について説明する。今回が本題である。
そもそも、Weldonに始まるメンデルのデータに対する疑問はこの「データが理論値に一致しすぎている」が発端である。前回取り上げた「1:1.7」問題はフィッシャーの疑念をより強めたポイントではあったが、それ単体で見れば「運が良かった」でも済ませられる程度のものであった。
フィッシャーの指摘
この問題における指摘の要点はこうだ。
「メンデルと同様の実験を行ったとき、メンデルと同等またはメンデルよりよい理論値への一致が得られるのは10万回に7回程度しかない」
具体的な計算はχ²値を用いて行われた。「雑種植物の研究」にメンデルは多くのデータを記載しているが、フィッシャーはそれらすべてについて(メンデルがデータ変動のために部分的に示した個体毎のデータも含めて)、χ²値を計算し上側確率を求めた。Fisher(1936)に記載されている表の内容を次に示す。

結論としては、84の自由度に対してχ² = 41.6056、対応する上側確率は0.99993というものであった*1。すなわち、分離比が理論どおりになるとすれば、実験を繰り返したときにメンデルの結果より理論値から外れた結果が得られる確率は0.99993ということである。これを逆に見れば、メンデルと同等以上の理論値に一致したデータは0.00007の確率でしか得られないということである。
そもそもχ²値をこのような使い方をしてよいのかという議論もあるのだが、ともあれ、この結果からフィッシャーは「メンデルのデータは期待値に一致しすぎている」という指摘をしている。
フィッシャーの指摘に対する説明たち
「データが一致しすぎている」に対しては、前回のように歯切れのよい説明は難しい。しかし、これまでにいくつかの説明が考えられている。主要なものは次の4つである。
- エンドウは分離比に影響する何らかの特性を持っている。これにより、分離比が自然に期待値に近接しやすい。
- 期待比率から大きく外れるデータが除外されている。
- あいまいな表現型を示す可能性がある形質の分類において、あいまいな表現型が都合よく分類されてしまった。
- 助手によるデータ操作があった。
これらの仮説は過去に何度も言及、検証されてはいるのだが、近年まで欠けていた視点としてエンドウの実際の遺伝的特性を踏まえた議論というものがある。これについて、エンドウの遺伝学者という立場からの視点を含めた検証を行った結果をまとめたのがWeedenの2016年の論文、"Are Mendel's Data Reliable? The Perspective of a Pea Geneticist"である。
今回はWeedenの論文を中心として、4つの説明それぞれについて解説していく。
1. エンドウは分離比を期待比率に近付ける何らかの特性をもつか?
エンドウの分離比は自然現象の結果であり、単純な統計モデルでは表現できない振る舞いを示す可能性を考慮しておく必要はあるだろう。もしかすると、二項分布が予想するより分散を減らす何らかのしくみがあるのかもしれない…。
この仮説は論争の比較的初期から存在していた。この仮説を説明するモデルとして代表的なものがテトラ花粉モデル(Tetrad-Pollen Model)と呼ばれているものである。このモデルは次のようなものだ。
- 花粉母細胞から花粉四分子が生ずるが、親植物がヘテロ接合型であれば、花粉四分子に含まれる半数体細胞は優性形質を含むものと劣性形質を含むものがそれぞれ2つずつとなっている。
- 花粉粒が成熟しても、花粉四分子の立体的配置が維持される。つまり、優性遺伝子を含む花粉と劣性遺伝子を含む花粉とが、3次元的に均等配置される。
- 均等配置が維持されたまま、花粉粒のサンプリングが起こる。その結果として、ランダムサンプリングが期待するのよりも分散が減少し、優性遺伝子と劣性遺伝子は1:1に近い比率でサンプリングされて柱頭に付着する。
- このサンプリング結果がさやの中の子世代の遺伝形質の分離にまで影響する。その結果として形質の分離比も期待値に近接する。
テトラ花粉モデルは40年以上にわたり、メンデルのデータの説明に用いられてきた。にもかかわらず、近年までテトラ花粉モデルはあくまで説にすぎず、具体的検証が行われていなかった。実験的検証の結果が報告されたのは2007年のことである。FairbanksとSchaaljeによるその論文は "The Tetrad-Pollen Model Fails to Explain the Bias in Mendel's Pea (Pisum sativum) Experiments" というタイトルである。
すでに出落ち感があるが、タイトルが示すようにテトラ花粉モデルはメンデルのデータのバイアス(ここでいうバイアスは理論値への近接を示していることに注意してほしい)を説明できなかった。実験では誤分類の可能性が低い形質として花の色を選び、973の自由度のもとで1003.58というχ²を得ており、対応するP値は0.2415であった。すべてのデータを合算して自由度1でP値を計算した場合はややP値が高くなるのだが、χ² = 0.0164に対しP = 0.8981であり、メンデルのデータに比べれば偶然の範疇と判断できる水準である*2。
すでに否定されている内容ではあるものの、Weedenはあらためてこの問題を遺伝学の知見を加えて検証した。Weedeが採用したアプローチは「過去の研究結果と比較する」というものである。このアプローチ自体は過去にも存在したが、Weedenは「分離比自体を調査対象とした研究を対象としない」という選択をした。これはどういうことかというと、分離比自体が調査対象である場合、実験者は(メンデルと同じように)期待比率を知っているため、メンデルと同様のバイアスが混入する危険性を避けられないためである。
「分離比自体が調査対象ではないが、分離比データが入っている」という都合のよい研究は何かというと、連鎖である。連鎖の研究では関心の対象は組み換え価にある。したがって、分離比が3:1であるかどうかはさほど重要ではなく、メンデルと同様のバイアスが入っている可能性は低いと考えられる。
Weedenは連鎖の研究データを数多く収集したが、一部は今回の調査対象から除外した。なぜなら、現代ではエンドウは一部の系統掛け合わせにおいて分離比が極端に偏るということが知られているためである。メンデルも実験手順の解説の記述から稔性による系統のスクリーニングをしていたことが伺えるため、このデータ選別自体大きな問題があるとは考えられない。また、メンデルにとっては有利に働くはずである。なお、データセットは元論文に補足資料として添付されているため、内容の確認は可能である。
データ分析の手法は先人のものと同様である。すなわち、各データセットについてχ²値と対応する上側確率を計算し、その分布を比較したのである。結果を次に示す。
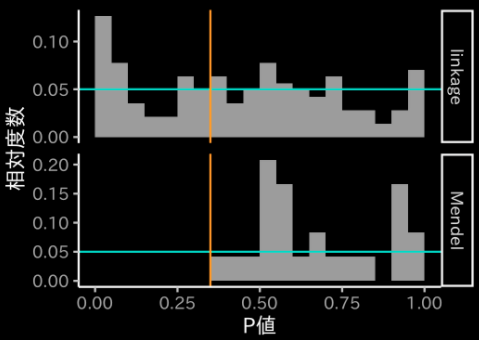
なお、論文中では過去の同様の調査結果であるJohannsen(1926)が収集したデータセットもプロットされているが、数が少ないため除外してある。
結果からは次のことが読み取れる。
すなわち、エンドウの分離比は自然と期待比率に一致する性質を持っていないし、むしろ、極端なデータを除外してもなおやや歪んだ比率を示す傾向を有する可能性があるということである。また、メンデルのデータはその性質を反映しておらず、極端なデータを除外した可能性が疑われる。
2. 期待比率から大きく外れるデータが除外されたか?
さきほどの調査結果からもすでにメンデルがデータの選別を行った可能性が示唆されるが、Weedenは加えて花序という形質に注目した。
花序は花が脇芽につく(腋生)か、頂芽につく(頂生)かという形質で、腋生が優性である。現代においては、エンドウの系統の組み合わせによっては花序の劣性形質の浸透度が100%とならないことがあること、またケースの多いことが知られている。浸透度というのは、表現型に対応する遺伝子を有している際に、実際にその表現型が現れる割合のことである。つまり、「劣性形質の浸透度が100%ではない」ということは、劣性ホモ接合型の個体が優性形質を示すケースがあるということだ。
もしこの現象がメンデルのデータに反映されていれば、優性形質の過剰という形で影響が現れるはずである。実際にはメンデルは花序について651:207 = 3.15:1という分離比を報告しており、大きな偏りが確認できない。すなわち、メンデルがデータ操作をしていなかったにしても、少なくとも浸透度が高い組み合わせを意図的に選別していた可能性が考えられる。
3. あいまいな表現型が都合よく分類されたか?
1対の対立形質は必ずしも常に明確に区別できる表現型として現れるわけではなく、ときにあいまいな表現型が生じてしまうケースがある。これはメンデルも認識しており、論文中でも言及している。しかし、メンデルは形質の区別について問題がなかったということを比較的はっきりと強調している。
まず、メンデルは実験に採用した形質はあいまいさの無いものだけであると記述している。
ここに挙げた形質の一部は確実、明確な識別ができず、識別はしばしば定義し難い「多少とも」という表現によるものであった。そのような形質は個々の実験には採用できないので、植物に明確、決定的に発現する形質のみに限った。
(メンデル著, 岩槻邦男・須原準平訳『雑種植物の研究』)
それでもなお場合によってはあいまいな例が生じることを認識しており、それにも言及している。しかし、そのような例は「選別の訓練をすれば」間違えることはないと述べている。
発育の途中で昆虫によって傷つけられた種子は、よく色と形が変わるが、ちょっと選別の訓練をすれば、誤りを避けることができる。
(メンデル著, 岩槻邦男・須原準平訳『雑種植物の研究』)
そして、メンデルの実験データには「判別不能」というカテゴリは存在せず、すべてのデータは必ず対立形質のいずれかに分類されている。
しかし、Weedenは表現型の分類がそれほど容易ではなく、メンデルが「明確に区別できる」として選定した形質の中にも判別が難しいものはあるとの指摘をしている。そうであれば、そこにはあいまいな形質を都合よく解釈してしまう(意図的かそうでないかにかかわらず)バイアスの入り込む余地がある。
Weedenはまずメンデルが扱った形質を「明確に判別できるもの」と「判別があいまいとなりうるもの」に分類した。
明確に判別できる形質は次の3つである。
- 草丈
- 種皮の色
- さやの色
これらの形質は違いが明瞭であり、またそれ単体で変化するわけではない。草丈は違いが明瞭であるのに加えて、背の高い形質では巻きひげが目立つ。種皮の色はアントシアニン合成経路の障害に関連しているため、透明な種皮は花色やアントシアニンの斑点と連動する。さやの色が黄色い個体は、さや以外の部分も黄色くなる。そしてこれらの特性についてはメンデルも言及している。
一方、判別があいまいとなりうる形質は次の4つである。
- 花序
- 種子の形状
- 子葉の色
- さやの形状
花序は先に説明したとおり浸透度の問題であり、中間型の形質があるわけではない。残り3つは中間型の形質を生ずる可能性がある。種子の形状(丸/しわ)は、丸い形質であっても発育不良でしわやへこみを生ずる場合がある。これについては種子内部のデンプン粒の形状観察がより正確な分類手法であるが、メンデルの時代には不明であった。子葉の色は発育不良で消えることがある。これはメンデルも認めている。また、当時は不明であった要因として、種皮の緑色要素に作用して色をあいまいにする遺伝子が存在する。さやの形状については後にReasmusson(1927)により草丈の遺伝子との間で組み換え価が調べられているが、その見積もりは5〜15cMと幅のあるものであった。これは表現型の分類の難しさに起因するとWeedenは推測している。なお、さやの形状と草丈の連鎖について気になると思うが、これは別の機会に再び取り上げる。
では、仮にあいまいな表現型が都合よく分類されたと仮定してみよう。そうであるなら、あいまいな表現型を生ずる形質は、明確に判別できる形質よりもより良く理論値に一致してしまっていると想定される。そこで、Weedenは次のようなアプローチをとった。
- メンデルのデータセットと連鎖研究由来のデータセットそれぞれについて、P値が0.5以上のものと0.5以下のものをカウントした。P値が0.5に等しいデータセットはそれぞれの階級に0.5個としてカウントした。
- もしデータにバイアスがなければP値は均一に分布すると期待できるので、P値0.5以上のデータセット数と0.5以下のデータセット数の期待比率を1:1としてχ²検定を行った。
結果を次に示す。

メンデルのデータセットのうちあいまいな表現型を生ずる形質のみが有意な偏差を示した。したがって、あいまいな形質に対して理論が予測する結果を(意図的にせよそうでないにせよ)反映した分類をしてしまった可能性が否定できない。
4. 助手がデータ操作をしたか?
この説も何度か取り上げられている。Novitski(1995)は、メンデルのデータは初期と後期でそれほど差がなく、実験開始前には期待結果を知らなかったはずであるからという理由でこの説に反対している。一方、フィッシャーはメンデルが先に理論を構築してから実験に取り組んだと考え、実験開始時点で助手に期待結果は伝えられていたと想定した。
メンデルは、茎の高さ、さやの色、さやの形状、花序という植物体を栽培しなければ調査できない形質を自分で調査し、種子で判別可能な形質については助手に任せたということが考えられている。もしそうであり、そのうえで助手が都合のよいデータ操作をしたのであれば、種子で判別可能な形質にバイアスが集中していると想定される。そこで、Weedenはさきほど「あいまいな表現型」仮説の際に用いた手法を、形質が種子で判別できるかどうかというグルーピングに対して適用した。結果を示す。
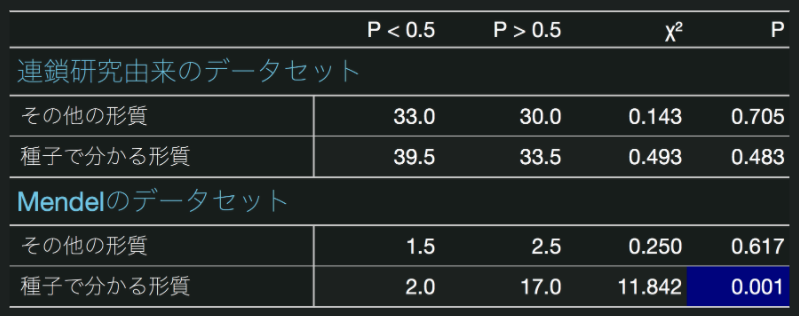
メンデルのデータセットのうち種子で判別されたものだけが有意な偏差を示している。したがって、この説も否定できないという結果となった。
「あいまいな表現型が都合よく分類された」「助手がデータを操作した」のいずれも否定できなかったが、これら2つの仮説についてどちらがよりありそうなのか比較は可能だろうか?
これについては種皮の色が鍵となる可能性があった。種皮の色は中間的な形質を生ずる可能性が低く、なおかつ種子の状態でも判別可能な形質である。もしこの形質に由来するデータがバイアスをもつなら「データ加工」仮説が有利であり、バイアスをもたないなら「あいまいな表現型」仮説が有利ということになる。しかし、種皮は花色でも判別できるため、メンデルが種皮形質を種子の状態で調査したデータは限られている。したがって、データセット数が十分ではなく、Weedenの検証内ではそこまでの判断はできなかった。
まとめ
「データが理論値に一致しすぎている」問題には主要な4つの説明があった。それぞれに対する結論を再度まとめよう。
- エンドウは分離比を期待比率に近付ける何らかの特性をもつか?
- この可能性は否定された。むしろ、エンドウの分離比は理論値よりも偏る傾向を示すことが多い。
- 期待比率から大きく外れるデータが除外されたか?
- これは可能性が高い。エンドウは形質の種類や系統の掛け合わせパターンによっては分離比が歪みやすい性質を示すが、メンデルのデータにはそのような例が欠如している。
- あいまいな表現型が都合よく分類されたか?
- あいまいな表現型は理論値に強く近接しており、可能性は否定できなかった。
- 助手がデータ操作をしたか?
- 助手が調査した可能性の高い種子形質のデータは理論値に近接しており、この可能性も否定できなかった。
結果としては、データ操作なしにメンデルの実験結果を再現する可能性のある仮説のみが否定され、それ以外の仮説は生き残った。これは「メンデルが捏造をした」にそのままつながるものではないが、少なくとも「論争は終わった」とは言えない状況だろう。
長くなったため、次の2点を次回に回す。
- メンデルはなぜ連鎖を発見できなかったのか。
- メンデルには極端なデータを省略して提示せざるを得ない動機、状況があったか。
参考文献
- メンデル著, 岩槻邦男・須原準平訳, (1999). 雑種植物の研究 (岩波文庫)
- Fairbanks, D. J., & Schaalje, G. B. (2007). The Tetrad-Pollen Model Fails to Explain the Bias in Mendel's Pea (Pisum sativum) Experiments. Genetics, 177(4), 2531 LP – 2534. https://doi.org/10.1534/genetics.107.079970
- Fisher, R. A. (1936). Has Mendel’s work been rediscovered? Annals of Science, 1(2), 115–137. https://doi.org/10.1080/00033793600200111
- Weeden, N. F. (2016). Are Mendel’s Data Reliable? The Perspective of a Pea Geneticist. Journal of Heredity, 107(7), 635–646. https://doi.org/10.1093/jhered/esw058
- メンデルの話 #2
- 今回の話を社内の勉強会で紹介した際のスライド。次回書く予定の内容も入っている。
次 → メンデルの法則をめぐる論争について (4) - 連鎖および近年のメンデルに対する評価
*1:この表はしばしば引用されており、たとえばC.R.ラオの「統計学とは何か」にも記載がある。これをもって同書籍内でメンデルが「悪者」にされているとの指摘を見たことがあるが、該当箇所を確認した限りではラオはフィッシャーの指摘を紹介しているのみであり、特に「悪者」扱いしているわけではない。むしろ、書籍内においてラオは「彼は今から120年前に,科学の歴史において初めて, "非決定論的規範" を導入したのである.」と高い評価をしており、扱いは肯定的である。ラオがメンデルを「悪者」扱いしているという指摘はラオに対して不当であろう。一方、ウィリアム・ブロードらによる「背信の科学者たち」のようにメンデルについて悪い印象を与えるような記述がされている書籍が存在するのもまた事実である。
*2:メンデルの法則の日本語版Wikipediaでは本稿執筆時点でこの論文を参照して「実験再現は、メンデルのデータに本当のバイアスがないことを実証している」との記述をしている。これは英語版のメンデルのページ(メンデルの法則のページではない)のテキストを直訳したものと思われるが、いささか誤解をまねく表現である。Fairbanks and Schaalje (2007)の結果にもとづくなら「再現実験の結果、メンデルのデータ中には本来のデータにあるべきバイアスが確認できなかった」とでもすべきだろう。ただ、そもそもこの論文はテトラ花粉モデルの検証が目的であり「メンデルの実験データにはバイアスが生じるべきであったかどうか」についてはそもそも言及しておらず、いずれにせよWikipediaの参照は適切とは言えない。